Bessel launches accelerator program for medtech startups
Bessel introduces accelerator program for medtech start-ups
cipbessel.com – Bessel and an Alabama technology center today said they are launching Hatch Powered by Bessel, an accelerator program for medtech start-ups.
Applications are currently open up for the 10-week program, which starts in Fairhope, Alabama, this summer.
The accelerator “combines the passion of start-up founders, the assistance of experienced clinical device experts, and the growing start-up community and financial investment in Alabama,” Bessel said in a press release. “… The program aims to gear up medtech start-ups to produce lasting and scalable innovations—breakthroughs that scale—and to give founders the entrepreneurial source community they need for long-lasting success.”
Start-ups selected for the program will receive a traveling stipend, access to occasions and workshops, and assistance on strategy, fundraising and implementation from lifescience industry business owners that will serve as coaches and advisors.
The start-ups may be offered financing for equity by Hatch Fairhope after the cohort wraps up with ending occasions in Fairhope, consisting of a demonstration day for the start-ups to pitch to financiers.
“There’s a skilled angel investor community that make effective clinical device financial investments and have the ability to follow their financial investments as the company progresses,” Bessel CEO Chris Danek informed MassDevice. “For instance, financiers in my start-up, AtheroMed, originated from this community.”
Hatch is a company center for tech-based business owners, moneyed by the Seaside Alabama Community University, the City of Fairhope, and the Baldwin Community + Financial Development Structure (BCEDF). The company helps its medtech start-ups access local scholastic health and wellness system USA Health and wellness Southern and the College of Alabama (UAB) Clinical Facility.
“Hatch take advantage of several local collaborations, and currently we can enter the medtech field through our collaboration with Bessel,” Hatch Experience Architect and Innovative Supervisor Keith Glines said in a press release. “Baldwin Region is such an innovation-rich community. The vibrant economic climate, job development, and access to considerable clinical and scholastic sources position Hatch Powered by Bessel for success.”
BESSEL FUNCTIONS ARISE IN MANY PROBLEMS

cipbessel.com – BESSEL FUNCTIONS ARISE IN MANY PROBLEMS in physics possessing cylindrical symmetry, such as the vibrations of circular drumheads and the radial modes in optical fibers. They also provide us with another orthogonal set of basis functions.
Bessel functions have a long history and were named after Friedrich Wilhelm Bessel ( \(1784-1846\) )
The first occurrence of Bessel functions (zeroth order) was in the work of Daniel Bernoulli on heavy chains (1738). More general Bessel functions. were studied by Leonhard Euler in 1781 and in his study of the vibrating membrane in \(1764 .\) Joseph Fourier found them in the study of heat conduction in solid cylinders and Siméon Poisson (1781-1840) in heat conduction of spheres ( 1823 ).
The history of Bessel functions, did not just originate in the study of the wave and heat equations. These solutions originally came up in the study of the Kepler problem, describing planetary motion. According to \(\mathrm{G} . \mathrm{N}\). Watson in his Treatise on Bessel Functions, the formulation and solution of Kepler’s Problem was discovered by Joseph-Louis Lagrange (1736-1813), in 1770. Namely, the problem was to express the radial coordinate and what is called the eccentric anomaly, \(E\), as functions of time. Lagrange found expressions for the coefficients in the expansions of \(r\) and \(E\) in trigonometric functions of time. However, he only computed the first few coefficients. In 1816, Friedrich Wilhelm Bessel \((1784-1846)\) had shown that the coefficients in the expansion for \(r\) could be given an integral representation. In 1824 , he presented a thorough study of these functions, which are now called Bessel functions.
You might have seen Bessel functions in a course on differential equations as solutions of the differential equation
\[x^{2} y^{\prime \prime}+x y^{\prime}+\left(x^{2}-p^{2}\right) y=0 \nonumber \]
Solutions to this equation are obtained in the form of series expansions.
Namely, one seeks solutions of the form
\[y(x)=\sum_{j=0}^{\infty} a_{j} x^{j+n} \nonumber \]
by determining the form the coefficients must take. We will leave this for a homework exercise and simply report the results.
One solution of the differential equation is the Bessel function of the first kind of order \(p\), given as
\[y(x)=J_{p}(x)=\sum_{n=0}^{\infty} \dfrac{(-1)^{n}}{\Gamma(n+1) \Gamma(n+p+1)}\left(\dfrac{x}{2}\right)^{2 n+p} \nonumber \]
Here \(\Gamma(x)\) s the Gamma function, satisfying \(\Gamma(x+1)=x \Gamma(x) .\) It is a generalization of the factorial and is discussed in the next section.
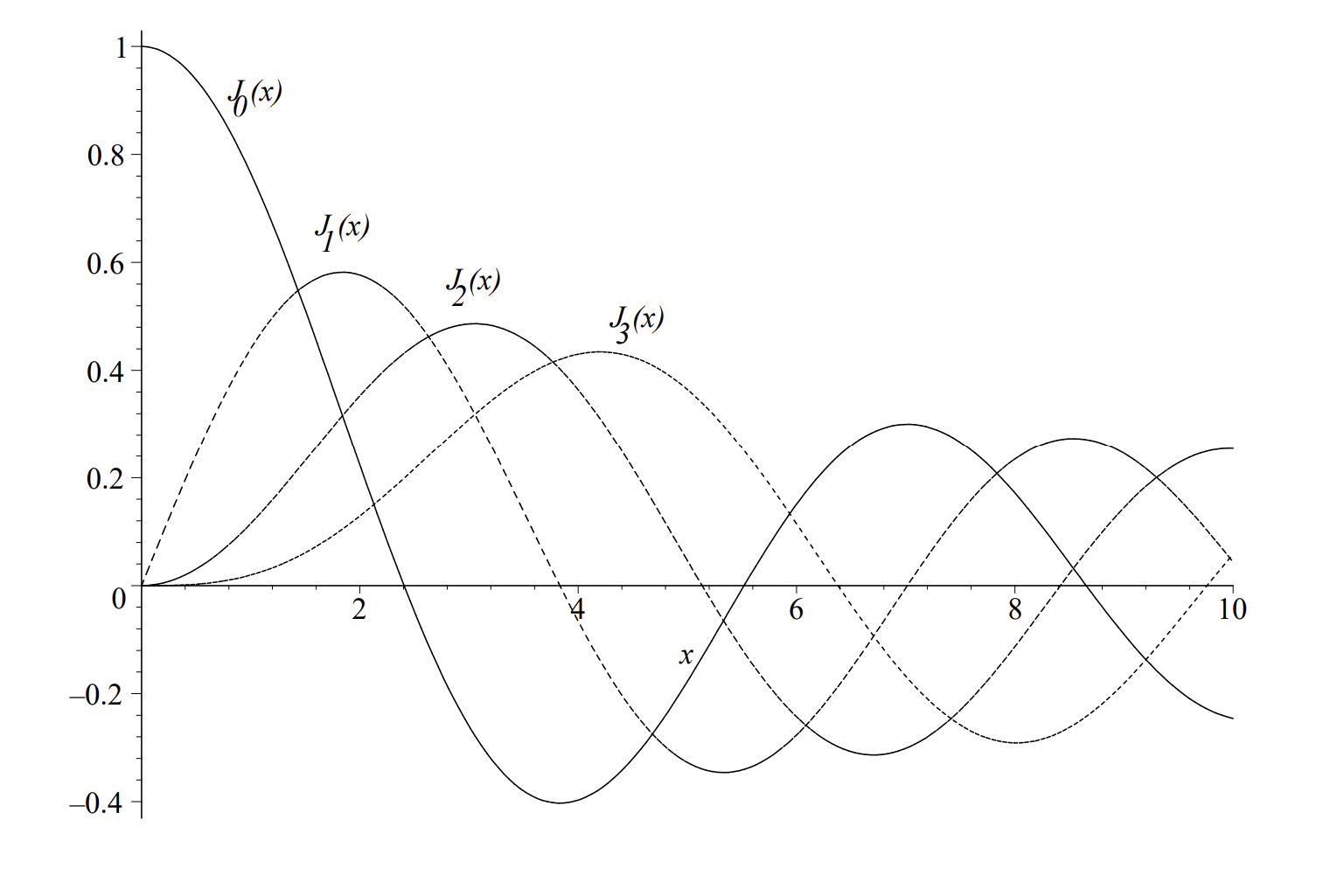
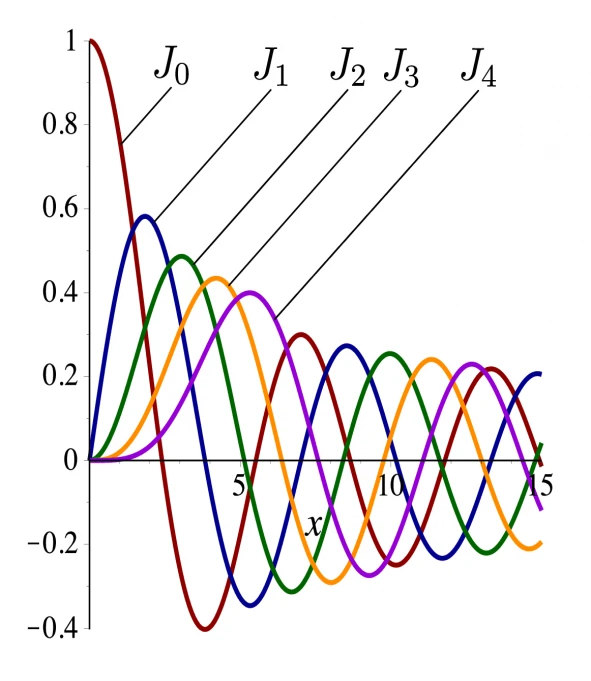
In Figure \(4.3\), we display the first few Bessel functions of the first kind of integer order. Note that these functions can be described as decaying oscillatory functions.
A second linearly independent solution is obtained for \(p\) not an integer as \(J_{-p}(x) .\) However, for \(p\) an integer, the \(\Gamma(n+p+1)\) factor leads to evaluations of the Gamma function at zero, or negative integers, when \(p\) is negative. Thus, the above series is not defined in these cases. Another method for obtaining a second linearly independent solution is through a linear combination of \(J_{p}(x)\) and \(J_{-p}(x)\) as
\[N_{p}(x)=Y_{p}(x)=\dfrac{\cos \pi p J_{p}(x)-J_{-p}(x)}{\sin \pi p} \nonumber \]
These functions are called the Neumann functions, or Bessel functions of the second kind of order \(p\).
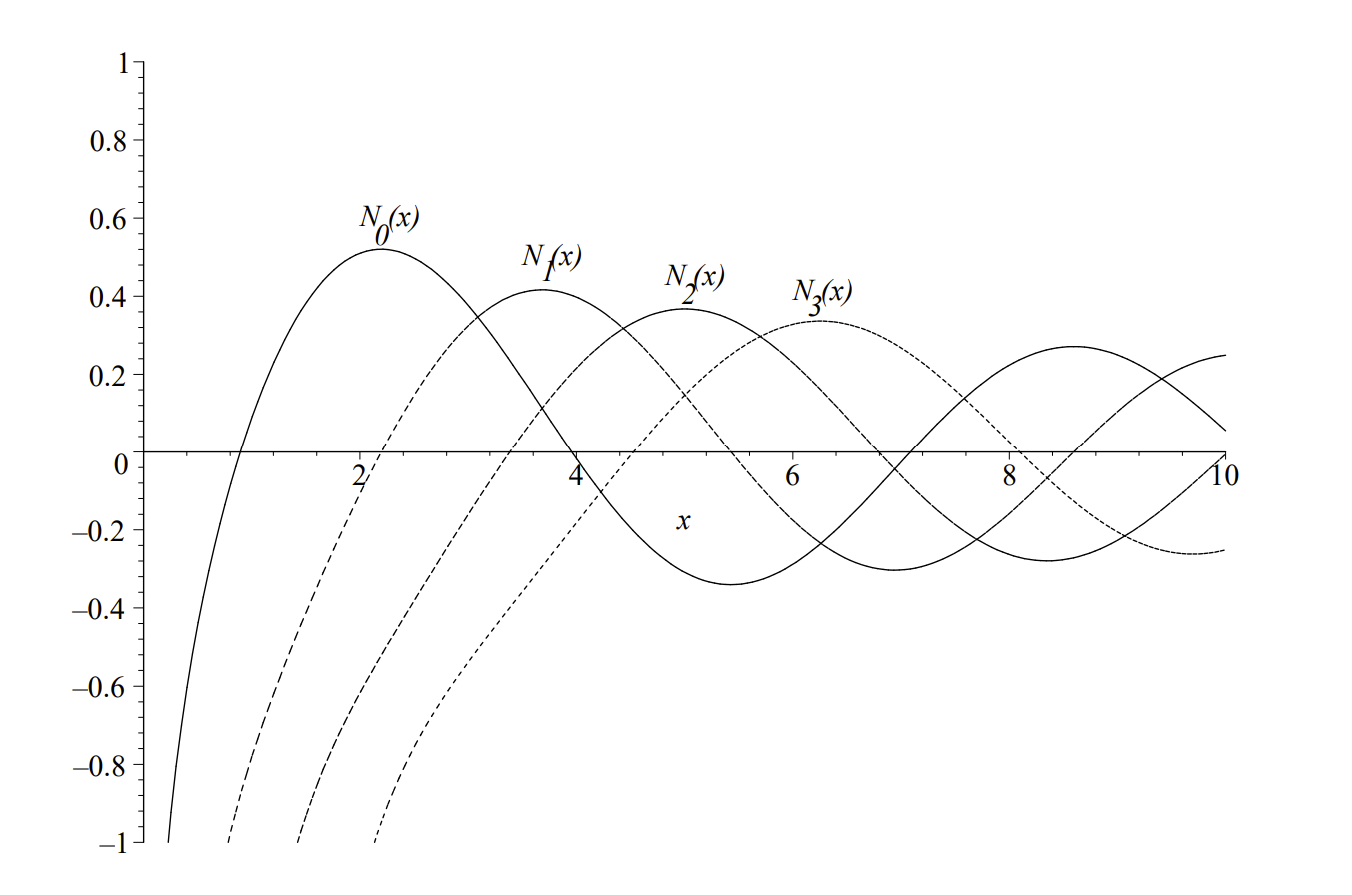
In Figure \(4.4\), we display the first few Bessel functions of the second kind of integer order. Note that these functions are also decaying oscillatory functions. However, they are singular at \(x=0\).
In many applications, one desires bounded solutions at \(x=0\). These functions do not satisfy this boundary condition. For example, one standard problem is to describe the oscillations of a circular drumhead. For this problem one solves the two dimensional wave equation using separation of variables in cylindrical coordinates. The radial equation leads to a Bessel equation. The Bessel function solutions describe the radial part of the solution and one does not expect a singular solution at the center of the drum. The amplitude of the oscillation must remain finite. Thus, only Bessel functions of the first kind can be used.
Bessel functions satisfy a variety of properties, which we will only list at this time for Bessel functions of the first kind. The reader will have the opportunity to prove these for homework.
Derivative Identities. These identities follow directly from the manipulation of the series solution.
\[ \dfrac{d}{d x}\left[x^{p} J_{p}(x)\right] =x^{p} J_{p-1}(x) \nonumber \]
\[\dfrac{d}{d x}\left[x^{-p} J_{p}(x)\right] =-x^{-p} J_{p+1}(x) \nonumber \]
Recursion Formulae. The next identities follow from adding, or subtracting, the derivative identities.
\[J_{p-1}(x)+J_{p+1}(x)=\dfrac{2 p}{x} J_{p}(x) \nonumber \]
\[J_{p-1}(x)-J_{p+1}(x)=2 J_{p}^{\prime}(x) \nonumber \]
Orthogonality. One can recast the Bessel equation into an eigenvalue problem whose solutions form an orthogonal basis of functions on \(L_{x}^{2}(0, a)\). Using Sturm-Liouville Theory, one can show that
\[\int_{0}^{a} x J_{p}\left(j_{p n} \dfrac{x}{a}\right) J_{p}\left(j_{p m} \dfrac{x}{a}\right) d x=\dfrac{a^{2}}{2}\left[J_{p+1}\left(j_{p n}\right)\right]^{2} \delta_{n, m} \nonumber \]
where \(j_{p n}\) is the \(n\)th root of \(J_{p}(x), J_{p}\left(j_{p n}\right)=0, n=1,2, \ldots\) A list of some of these roots is provided in Table \(\PageIndex{1}.\)
| \(n\) | \(m=0\) | \(m=1\) | \(m=2\) | \(m=3\) | \(m=4\) | \(m=5\) |
|---|---|---|---|---|---|---|
| 1 | \(2.405\) | \(3.832\) | \(5.136\) | \(6.380\) | \(7.588\) | \(8.771\) |
| 2 | \(5.520\) | \(7.016\) | \(8.417\) | \(9.761\) | \(11.065\) | \(12.339\) |
| 3 | \(8.654\) | \(10.173\) | \(11.620\) | \(13.015\) | \(14.373\) | \(15.700\) |
| 4 | \(11.792\) | \(13.324\) | \(14.796\) | \(16.223\) | \(17.616\) | \(18.980\) |
| 5 | \(14.931\) | \(16.471\) | \(17.960\) | \(19.409\) | \(20.827\) | \(22.218\) |
| 6 | \(18.071\) | \(19.616\) | \(21.117\) | \(22.583\) | \(24.019\) | \(25.430\) |
| 7 | \(21.212\) | \(22.760\) | \(24.270\) | \(25.748\) | \(27.199\) | \(28.627\) |
| 8 | \(24.352\) | \(25.904\) | \(27.421\) | \(28.908\) | \(30.371\) | \(31.812\) |
| 9 | \(27.493\) | \(29.047\) | \(30.569\) | \(32.065\) | \(33.537\) | \(34.989\) |
Generating Function.
\[e^{x\left(t-\dfrac{1}{t}\right) / 2}=\sum_{n=-\infty}^{\infty} J_{n}(x) t^{n}, \quad x>0, t \neq 0 \nonumber \]
Integral Representation.
\[J_{n}(x)=\dfrac{1}{\pi} \int_{0}^{\pi} \cos (x \sin \theta-n \theta) d \theta, \quad x>0, n \in Z \nonumber \]

Generasi sinar Bessel-Gaussian dalam chip untuk penginderaan jarak jauh
Generasi sinar Bessel-Gaussian dalam chip untuk penginderaan jarak jauh
Sinar Bessel, dengan kedalaman bidang yang signifikan dan karakteristik penyembuhan diri, telah diterapkan dalam aplikasi yang luas, termasuk keterikatan kuantum, pencitraan 3D bawah air, manipulasi mikro optik, mikroskop, dan sebagainya. Namun, metode ini, seperti celah melingkar dan lensa, akson, modulator cahaya spasial (SLM), rumit karena penggunaan elemen optik yang besar dan menghalangi penerapan sistem pembangkitan sinar Bessel dalam aplikasi praktis.
Baru-baru ini, beberapa sistem kompak telah diusulkan untuk menghasilkan sinar Bessel dengan menggunakan sirkuit terpadu fotonik (https://cipbessel.com/), permukaan meta, pandu gelombang terintegrasi, dan serat cetak 3D. Namun jarak rambat sinar Bessel yang dihasilkan oleh teknologi di atas pendek, sehingga secara signifikan membatasi penerapan sinar Bessel dalam skenario yang memerlukan jarak rambat yang jauh.
Karya baru yang diterbitkan di Light: Science & Applications
Dalam karya baru yang diterbitkan di Light: Science & Applications , tim ilmuwan, dipimpin oleh Profesor Junfeng Song dari State Key Laboratory on Integrated Optoelectronics, College of Electronic Science and Engineering, Jilin University, Changchun, China, Peng Cheng Laboratory, Shenzhen, Tiongkok dan rekan kerjanya telah mengusulkan struktur yang belum pernah ada sebelumnya berdasarkan susunan kisi fotonik silikon untuk menghasilkan sinar Bessel Gaussian (BGb) dengan jarak propagasi yang jauh (diukur 10,24 m).
Susunan kisi didistribusikan secara konsentris pada chip. Selain itu, diperoleh profil BGb yang dioperasikan pada rentang panjang gelombang dari 1500 nm hingga 1630 nm. Distribusi spasial intensitas cahaya mengikuti fungsi Bessel jenis pertama. Terakhir, para peneliti juga menerapkan BGb terpolarisasi azimuth untuk mengukur kecepatan rotasi dan jarak target secara bersamaan.
Dengan ukuran yang ringkas, biaya rendah, dan potensi produksi massal dari proses terintegrasi, metode dan teknik yang dilaporkan menjanjikan untuk memungkinkan sinar Bessel-Gaussian dalam komunikasi optik luas dan aplikasi manipulasi mikro.
Kelompok ini merangkum prinsip chip fotonik silikon terintegrasi untuk menghasilkan sinar Bessel-Gaussian jarak jauh:
“BGb dapat diperoleh dengan superposisi rangkaian berkas Gaussian. Prosesnya tidak hanya terkait dengan sudut pancaran, tetapi juga dengan divergensi setengah sudut berkas Gaussian. Karena koherensi antara berkas Gaussian dan simetri Dari distribusi melingkar, balok Bessel-Gaussian terbentuk pada area yang tumpang tindih. Sudut emisi dan sudut divergensi berkas Gaussian menentukan posisi spasial dari area yang tumpang tindih. Secara teori, area yang tumpang tindih bisa mencapai tak terhingga.”
Selanjutnya, untuk menghasilkan BGb jarak jauh, struktur pandu gelombang dirancang dengan cermat, terutama lebar susunan kisi dan periode kisi. Kami telah melakukan banyak simulasi, dan akhirnya menentukan ukurannya. Seluruh struktur cincin memiliki diameter 870 μm, dan pemancar kisi 64 saluran yang disusun secara melingkar. Chip fotonik dibuat pada substrat silikon-on-isolator (SOI) dengan proses CMOS 130 nm 8 inci standar Singapore Advanced Micro Foundry (AMF).
Rotasi adalah fenomena mendasar di alam dan pendekatan yang efektif untuk mengukur kecepatan rotasi sangat penting untuk mengungkap karakteristik fisika, mengelola mesin yang tepat, dan menganalisis komposisi benda langit. Untuk mendemonstrasikan fungsi BGb yang dihasilkan, kami juga mengukur kecepatan rotasi secara eksperimental. objek berputar melalui Efek Doppler rotasi dan jarak melalui prinsip jangkauan laser fase. BGb pada chip dapat memberikan solusi terintegrasi untuk pengukuran rotasi yang efektif.”
“Karena luas perangkat ini kurang dari 1 milimeter persegi, dan biaya satu perangkat akan dikurangi menjadi kurang dari 50 sen dalam produksi massal. Generator BGb on-chip yang berbiaya rendah, berkualitas tinggi, dan jarak jauh ini adalah kunci dari sinar Bessel masa depan dalam skenario aplikasi berskala besar, mini, dan sangat stabil,” tambah mereka.